Example 10: Bidimensional Fuzzy Entropy

Import an image of a Mandelbrot fractal as a matrix.

X = ExampleData('mandelbrot_Mat');

figure('Color','k'),
imshow(X,[],'InitialMagnification',500),
colormap('hot')

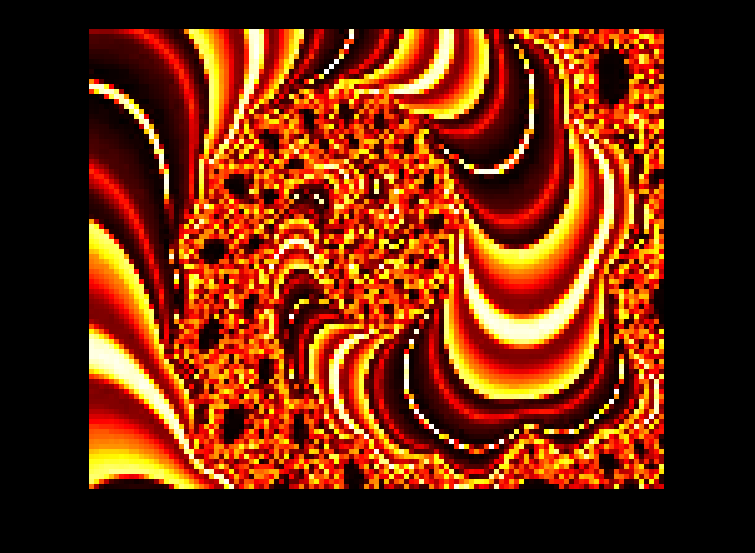
https://github.com/MattWillFlood/EntropyHub/blob/main/Graphics/mandelbrot.png?raw=true

Calculate the bidimensional fuzzy entropy in trits (logarithm base 3) with a template matrix of size [8 x 5], and a time delay (tau) of 2 using a 'linear' fuzzy function with distances linearly normalised to the range [0, 1]:

\[f(x) = exp(- \frac{x - x_{min}}{x_{max} - x_{min}})\]

FE2D = FuzzEn2D(X, 'm', [8 5], 'tau', 2, 'Fx', 'linear', 'r', 0, 'Logx', 3)

>>> FE2D =
    0.0016