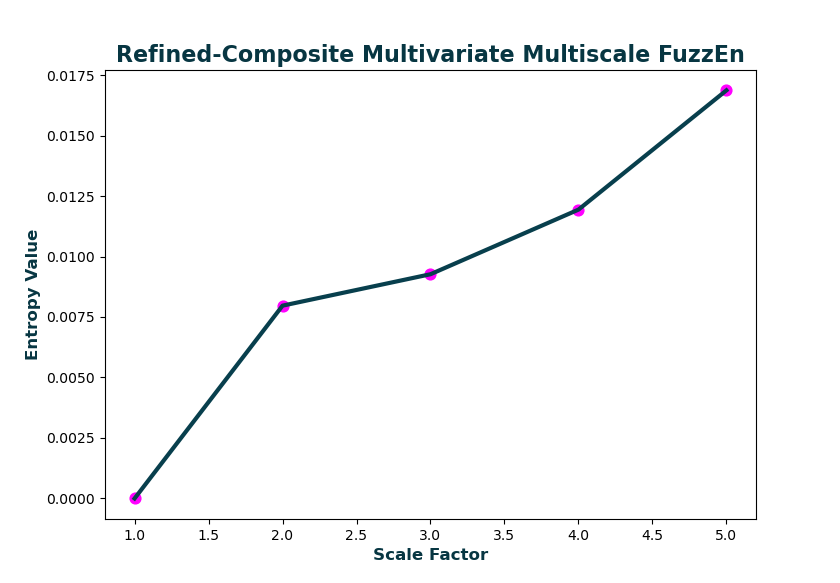
Example 12: [Generalized] Refined-composite Multivariate Multiscale Fuzzy Entropy

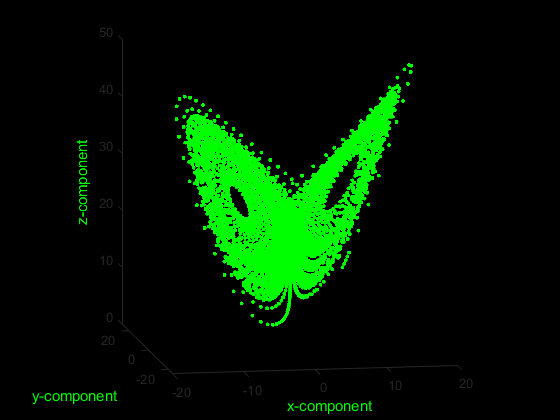
Import the x, y, and z components of the Lorenz system of equations.

Data = ExampleData('lorenz');

figure('Color', 'k')
plot3(Data(:,1), Data(:,2), Data(:,3), 'g.')
xlabel('x-component','color','g'),
ylabel('y-component','color','g'),
zlabel('z-component','color','g'),
view(-10,10), set(gca,'color','k'), axis square

Create a multiscale entropy object with the following parameters: EnType = MvFuzzEn(), fuzzy membership function = ‘constgaussian’, fuzzy function parameter = 1.75, normalized data to unit variance = true.

Mobj = MSobject('MvFuzzEn', 'Fx', 'constgaussian', 'r', 1.75, 'Norm', true)

Calculate the generalized refined-composite multivariate multiscale fuzzy entropy over 5 scales and plotting the output.

Hint

When the multivariate entropy method is multivariate fuzzy entropy (MvFuzzEn), cMvMSEn by default employs a generalized graining procedure with the standard deviation (not the variance like in MvMSEn). This follows the method presented in [1].

[1] Azami, Fernández and Escudero. ” Refined multiscale fuzzy entropy based on standard deviation for biomedical signal analysis ” Medical & biological engineering & computing 55 (2017): 2037-2052

Caution

As with conventional generalized multiscale entropy, the multiscale entropy value for the first scale will always == 0, as the variance or standard deviation of a singular value is 0!

[MSx, CI] = cMvMSEn(Data, Mobj, 'Scales', 5, 'Refined', true, 'Plotx', true)

>>> MSx =
    0,  0.00796833,  0.00926765,  0.01193731,  0.01686631

>>> RDE =
    0.04603960