Example 9: Hierarchical Multiscale corrected Cross-[Conditional] Entropy

Import the x and y components of the Henon system of equations and create a multiscale entropy object with the following parameters:

EnType = XCondEn(), embedding dimension = 2, time delay = 2, number of symbols = 12, logarithm base = 2, normalization = true

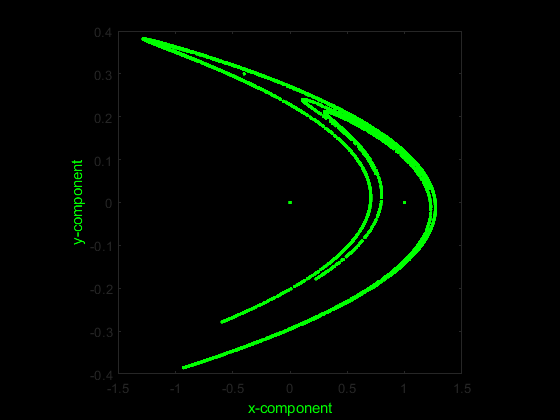
Data = ExampleData('henon');

figure('Color', 'k')
plot(Data(:,1), Data(:,2), 'g.')
xlabel('x-component','color','g')
ylabel('y-component','color','g')
set(gca,'color','k'), axis square

Mobj = MSobject('XCondEn', 'm', 2, 'tau', 2, 'c', 12, 'Logx', 2, 'Norm', true)

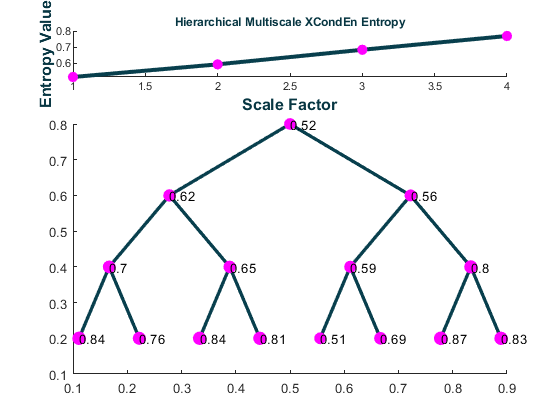
Calculate the hierarchical multiscale corrected cross-conditional entropy over 4 temporal scales and return the average cross-entropy at each scale (Sn), the complexity index (Ci), and a plot of the multiscale entropy curve and the hierarchical tree with the cross-entropy value at each node.

[MSx, Sn, Ci] = hXMSEn(Data(:,1), Data(:,2), Mobj, 'Scales', 4, 'Plotx', true)

>>> Only first 4096 samples were used in hierarchical decomposition.
>>> The last 404 samples of each data sequence were ignored.

>>> MSx = 1×15
    0.5159 0.6245 0.5634 0.7022 0.6533
    0.5853 0.7956 0.8447 0.7605 0.8415
    0.8115 0.5128 0.6862 0.8679 0.8287

    Sn = 1×4
    0.5159 0.5940 0.6841 0.7692

    Ci =
    2.5632